சாட்ஜிபிடி உள்ளிட்ட செயற்கை நுண்ணறிவு சேவைகளின் செயல்பாட்டை புரிந்து கொள்ள வேண்டும் எனில், இயந்திர அறிவிற்காக பயன்படுத்தப்படும் சில அடிப்படையான கோட்பாடுகளை புரிந்து கொள்ள வேண்டும். இவற்றில் மார்கோவ் தொடர் கருத்தாக்கம் முக்கியமானது.
மார்கோவ் தொடர் செயற்கை நுண்ணறிவு துறையில் பரவலாக பயன்படுத்தப்படுவது, மிகவும் எளிமையானது. இது இஷடம் போல தோன்றும் நிலைகளை புள்ளியல்படி கணிக்க உதவுகிறது.
வானிலை கணிப்பு துவங்கி, எழுத்து உருவாக்கம் வரை பல துறைகளில் மார்கோவ் தொடர் பயன்படுகிறது.
மார்கோவ் தொடர் செயல்பாட்டை புரிந்து கொள்ள ஒரு எளிய உதாரணத்தை பார்க்கலாம்.
வானிலையை எடுத்துக்கொள்வோம். மேக மூட்டம் மிக்கது அல்லது நன்றாக வெயில் காய்வது என ஒரு நிலைகள் இருப்பதாக வைத்துக்கொள்வோம். தற்போது வானிலை என்ன என்பதை எப்போதும் எளிதாக தெரிந்து கொள்ளலாம். வீட்டை விட்டு வெளியே வந்து பார்த்தால், வானிலை மேகமூட்டமா? அல்லது வெயிலா என தெரிந்து கொள்ளலாம்.
தற்போதைய வானிலை அடிப்படையில் நாளைய வானிலை என்பது, இரண்டு நிலையில் ஒரு நிலை தான் என்பதையும் எளிதாக யூகித்துவிடலாம். அதாவது ஒன்று, வெயில் காய்ந்தால், நாளை வெயில் காயலாம் அல்லது மேகமூட்டமாக இருக்கலாம்.
ஆக, நாளைய வானிலையை இன்றைய வானிலை கொண்டு கணிக்கலாம் எனில், அடுத்து வரும் நாட்களின் வானியையும் கணிக்கலாம் அல்லவா? இதற்கு நாம் என்ன செய்ய வேண்டும் எனில் கடந்த காலங்கில், வானிலை மாற்றம் எப்படி நிகழ்ந்து வந்துள்ளன எனும் தரவுகளை சேகரித்தால், வெயிலுக்கு மறு நாள் வெயில் தோன்றும் வாய்ப்பு எத்தனை சதவீதம் என தெரிந்து கொள்ளலாம். அதே அடிப்படையில், வெயிலுக்கு மறுநாள் மேகமூட்டம் தோன்றும் சாத்தியத்தையும் கணக்கிடலாம்.
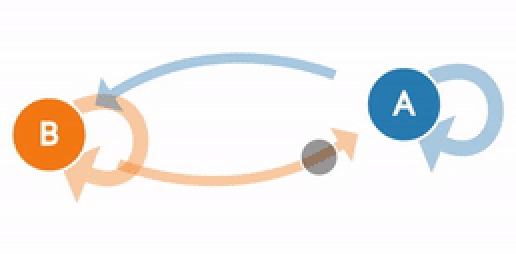
இப்போது இந்த தரவுகளில் வெயிலுக்கும், மேகமூட்டத்திற்குமான நிலை மாற்றத்தின் அமைப்பை வைத்துக்கொண்டு அதே அடிப்படையில் வரும் நாட்களுக்கான வானிலையையும் கணிக்கலாம்.
இதில் முக்கியமான விஷயம் என்னவெனில், இந்த கணிப்பில் தற்போதைய நிலை தான் அடிப்படை. அதற்கு முந்தைய நிலை அல்ல. இப்படி, கடந்த கால நிலைகளின் தாக்கம் இல்லாமல், தற்போதைய நிலை அடிப்படையிலேயே எதிர்கால நிலை அமைகிறது என்பது மார்கோவ் தொடரின் முக்கிய அம்சம். இந்த அம்சம் கொண்ட எந்த நிலை மாற்றத்தையும் மார்கோவ் தொடர் கோட்பாடு மூலம் கணித்துவிடலாம்.
கடந்த கால நிலையின் தாக்கம் இல்லாதது மார்கோவ் தொடரை நினைவு சார்ந்ததாக இல்லாமல் செய்கிறது. எனவே, ஒரு நிலைமாற்றத்தை மார்கோவ் தொடர் கொண்டு எளிதாக கணிக்கலாம். இதே முறையில், ஒரு எழுத்தாளரின் ஆக்கங்களில் குறிப்பிட்ட எழுத்துக்கள் தோன்றும் வரிசையை வைத்து அவரது எழுத்து போலவே எழுதக்கூடிய ஒரு நிரலை உருவாக்கலாம். ஆனால், அந்த எழுத்தில் உள்ளார்ந்திருக்கும் பொருளை கொண்டு வர முடியாது.
மார்கோவ் தொடரை செயல்படுத்த எளிய கணித சூத்திரங்களும் இருக்கின்றன. மார்கோவ் தொடரின் அடுத்த நிலையாக உள்ளார்ந்த பொருளை வெளிக்கொணர உதவும் மறைந்திருக்கும் அம்சமும் இருக்கிறது.
மார்கோவ் தொடர் பற்றிய மூலக்கட்டுரை: https://towardsdatascience.com/introduction-to-markov-chains-50da3645a50d

சாட்ஜிபிடி உள்ளிட்ட செயற்கை நுண்ணறிவு சேவைகளின் செயல்பாட்டை புரிந்து கொள்ள வேண்டும் எனில், இயந்திர அறிவிற்காக பயன்படுத்தப்படும் சில அடிப்படையான கோட்பாடுகளை புரிந்து கொள்ள வேண்டும். இவற்றில் மார்கோவ் தொடர் கருத்தாக்கம் முக்கியமானது.
மார்கோவ் தொடர் செயற்கை நுண்ணறிவு துறையில் பரவலாக பயன்படுத்தப்படுவது, மிகவும் எளிமையானது. இது இஷடம் போல தோன்றும் நிலைகளை புள்ளியல்படி கணிக்க உதவுகிறது.
வானிலை கணிப்பு துவங்கி, எழுத்து உருவாக்கம் வரை பல துறைகளில் மார்கோவ் தொடர் பயன்படுகிறது.
மார்கோவ் தொடர் செயல்பாட்டை புரிந்து கொள்ள ஒரு எளிய உதாரணத்தை பார்க்கலாம்.
வானிலையை எடுத்துக்கொள்வோம். மேக மூட்டம் மிக்கது அல்லது நன்றாக வெயில் காய்வது என ஒரு நிலைகள் இருப்பதாக வைத்துக்கொள்வோம். தற்போது வானிலை என்ன என்பதை எப்போதும் எளிதாக தெரிந்து கொள்ளலாம். வீட்டை விட்டு வெளியே வந்து பார்த்தால், வானிலை மேகமூட்டமா? அல்லது வெயிலா என தெரிந்து கொள்ளலாம்.
தற்போதைய வானிலை அடிப்படையில் நாளைய வானிலை என்பது, இரண்டு நிலையில் ஒரு நிலை தான் என்பதையும் எளிதாக யூகித்துவிடலாம். அதாவது ஒன்று, வெயில் காய்ந்தால், நாளை வெயில் காயலாம் அல்லது மேகமூட்டமாக இருக்கலாம்.
ஆக, நாளைய வானிலையை இன்றைய வானிலை கொண்டு கணிக்கலாம் எனில், அடுத்து வரும் நாட்களின் வானியையும் கணிக்கலாம் அல்லவா? இதற்கு நாம் என்ன செய்ய வேண்டும் எனில் கடந்த காலங்கில், வானிலை மாற்றம் எப்படி நிகழ்ந்து வந்துள்ளன எனும் தரவுகளை சேகரித்தால், வெயிலுக்கு மறு நாள் வெயில் தோன்றும் வாய்ப்பு எத்தனை சதவீதம் என தெரிந்து கொள்ளலாம். அதே அடிப்படையில், வெயிலுக்கு மறுநாள் மேகமூட்டம் தோன்றும் சாத்தியத்தையும் கணக்கிடலாம்.
இப்போது இந்த தரவுகளில் வெயிலுக்கும், மேகமூட்டத்திற்குமான நிலை மாற்றத்தின் அமைப்பை வைத்துக்கொண்டு அதே அடிப்படையில் வரும் நாட்களுக்கான வானிலையையும் கணிக்கலாம்.
இதில் முக்கியமான விஷயம் என்னவெனில், இந்த கணிப்பில் தற்போதைய நிலை தான் அடிப்படை. அதற்கு முந்தைய நிலை அல்ல. இப்படி, கடந்த கால நிலைகளின் தாக்கம் இல்லாமல், தற்போதைய நிலை அடிப்படையிலேயே எதிர்கால நிலை அமைகிறது என்பது மார்கோவ் தொடரின் முக்கிய அம்சம். இந்த அம்சம் கொண்ட எந்த நிலை மாற்றத்தையும் மார்கோவ் தொடர் கோட்பாடு மூலம் கணித்துவிடலாம்.
கடந்த கால நிலையின் தாக்கம் இல்லாதது மார்கோவ் தொடரை நினைவு சார்ந்ததாக இல்லாமல் செய்கிறது. எனவே, ஒரு நிலைமாற்றத்தை மார்கோவ் தொடர் கொண்டு எளிதாக கணிக்கலாம். இதே முறையில், ஒரு எழுத்தாளரின் ஆக்கங்களில் குறிப்பிட்ட எழுத்துக்கள் தோன்றும் வரிசையை வைத்து அவரது எழுத்து போலவே எழுதக்கூடிய ஒரு நிரலை உருவாக்கலாம். ஆனால், அந்த எழுத்தில் உள்ளார்ந்திருக்கும் பொருளை கொண்டு வர முடியாது.
மார்கோவ் தொடரை செயல்படுத்த எளிய கணித சூத்திரங்களும் இருக்கின்றன. மார்கோவ் தொடரின் அடுத்த நிலையாக உள்ளார்ந்த பொருளை வெளிக்கொணர உதவும் மறைந்திருக்கும் அம்சமும் இருக்கிறது.
மார்கோவ் தொடர் பற்றிய மூலக்கட்டுரை: https://towardsdatascience.com/introduction-to-markov-chains-50da3645a50d